Solids: Volume calculation, centroid coordinates

Here you will find formulas for determining the volume contents and centroid coordinates of simple solids. This information will assist you, for example, in determining the centroid of composite solids composed of simple subregions.

Solids: Volume calculation, centroid coordinates

Table 1: Volume and centroid coordinates of solids
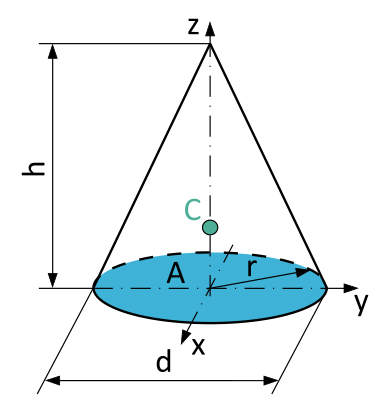
Conical solids 		Cone Abb. $$\begin{align}V&=\dfrac{A \cdot h}{3}\\A&=r^2 \cdot \pi=\dfrac{d^2 \cdot \pi}{4}\\V&=\dfrac{1}{3} \cdot r^2 \cdot \pi \cdot h\\V&=\dfrac{1}{3} \cdot \dfrac{d^2 \cdot \pi}{4} \cdot h\end{align}$$ $$\begin{align}C_x &= 0\\[7pt]C_y &= 0\\[7pt] C_z &= \dfrac{1}{4} \cdot h\end{align}$$
  • \(C:\) Centroid
  • \(r:\) Radius
  • \(d:\) Diameter
  • \(C_x:\) Centroid coordinate
  • \(C_y:\) Centroid coordinate
  • \(C_z:\) Centroid coordinate
  • \(A:\) Area
  • \(V:\) Volume