Rigid Body Statics

Fundamentals: Are you ready to explore the world of rigid bodies?

In this chapter, we will dive into the fascinating world of rigid body mechanics and explore:

  • The invisible forces that act on objects and set them in motion or slow them down.
  • The secret of cutting free, which allows us to isolate the most important forces acting on an object.
  • The magical free body diagrams, which show us how forces and moments act on an object.
  • The rigid body and its six degrees of freedom, which give it its mobility.
  • The 6 axioms of rigid body statics, which are the foundation for everything we know about objects at rest.

Are you ready to uncover these secrets?

Then buckle up and let's go on an exciting journey into the world of rigid body mechanics!

It's going to be exciting!

On this Page
Table of Contents

4.4 The Superposition Principle

Balancing Act

Today we dive into the world of equilibrium groups, a topic that might not seem exciting at first glance. But don't be fooled, there's more excitement here than you think!

Imagine a variety of forces acting on a rigid body. These forces can point in any direction and have different strengths. Now here's the kicker: you can add as many additional forces as you want, as long as they balance each other out and don't affect the effect of the first group. Fascinating, right?

Such a group of "balancing" forces is called an equilibrium group. It's similar to tug-of-war: both teams pull with equal force, and nobody moves.

The Superposition Game

Let's imagine we have a rigid body, e.g. a beam, on which some forces are acting.

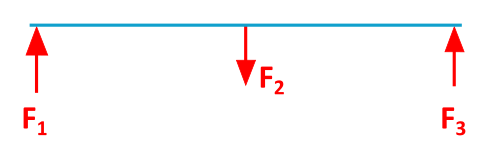
This figure 2.4.7 shows a beam loaded with an arbitrary force group F1, F2, and F3.
Fig. 2.4.7: Beam with force group

Now here's the cool part: we can attach as many ropes or struts to this beam as we want, and they won't affect the effect of the existing forces. We can even attach these additional forces to the beam wherever we want! The only condition is that each new force group (rope and/or strut) must form an equilibrium group by itself. And this works even if we superimpose more than two forces as an equilibrium group. Crazy, right?

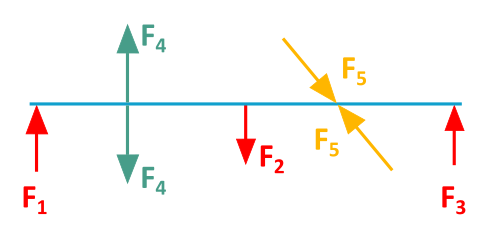
This figure 2.4.7 shows a beam loaded with an arbitrary force group F1, F2, and F3 and additionally with two equilibrium groups with forces F4 and F5.
Fig. 2.4.8: Beam with force group and superimposed equilibrium groups
Why does this work?

It's because an equilibrium group, by definition, has no "force" in the real sense. The individual forces in the group cancel each other out. It's as if they're holding each other back.

What's the point?

The principle of equilibrium groups is crucial for understanding the physics of forces. For example, you can use it to break down complex force effects into simpler parts and calculate them. Because the reverse is also true: you can remove equilibrium groups without affecting the effect of the overall system.

Conclusion:

Equilibrium groups are like invisible helpers in the world of physics. They make sure that everything doesn't descend into chaos. And by the way, they're proof that it's okay to "do nothing" sometimes, without anything bad happening.